Question

A right triangle has side lengths ac = 7 inches, bc = 24 inches, and ab = 25 inches. What are the measures of the angles in triangle abc?

1) m∠a ≠ˆ 46.2°, m∠b ≠ˆ 43.8°, m∠c ≠ˆ 90°
2) m∠a ≠ˆ 73.0°, m∠b ≠ˆ 17.0°, m∠c ≠ˆ 90°
3) m∠a ≠ˆ 73.7°, m∠b ≠ˆ 16.3°, m∠c ≠ˆ 90°
4) m∠a ≠ˆ 74.4°, m∠b ≠ˆ 15.6°, m∠c ≠ˆ 90°

Answer 1

A right triangle has side lengths ac = 7 inches, bc = 24 inches, and ab = 25 inches.Measures of the angles in triangle abc are 3)
`\(m∠a \\eq 73.7°\), \(m∠b \\eq 16.3°\), \(m∠c \\eq 90°\)`

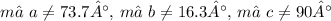
Step-by-step explanation:

In a right triangle, the angles can be determined using trigonometric ratios. Given the side lengths
`\(a = 7\), \(b = 24\), and \(c = 25\)` , where
`\(c\)` is the hypotenuse, the cosine of angle
`\(A\) (\(∠a\)) i`s given by
`\(\cos(A) = (a)/(c)\).`

`\(\cos(A) = (a)/(c)\).`

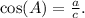
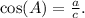
Using the inverse cosine function, we can find the measure of angle
`\(A\):`

`\[ A = \cos^(-1)\left((7)/(25)\right) \approx 73.7° \]`

Similarly, angle
`\(B\) (\(∠b\))` can be found using the sine ratio:

`\[ \sin(B) = (a)/(c) \]`

`\[ B = \sin^(-1)\left((7)/(25)\right) \approx 16.3° \]`

Since it is a right triangle, the sum of angles
`\(A\) and \(B\)` should equal
`\(90°\),`making angle
`\(C\) (\(∠c\)) \(90°\).`

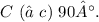
Therefore, the correct answer is option 3, where
`\(m∠a \\eq 73.7°\), \(m∠b \\eq 16.3°\),` and
`\(m∠c \\eq 90°\).`This corresponds to the angles calculated using trigonometric ratios in a right triangle with side lengths
`\(7\), \(24\), and \(25\)`inches.