Question

You intend to estimate a population mean μ with the following sample. 56.1 27 40.9 38.9 30.3 36.5 34.5 50 45 you believe the population is normally distributed. find the 80% confidence interval. enter your answer as an open-interval (i.e., parentheses) accurate to twp decimal places (because the sample data are reported accurate to one decimal place).

Answer 1

The 80% confidence interval for the population mean (μ) is (32.70, 45.10).

Step-by-step explanation:

To calculate the 80% confidence interval for the population mean (μ), we can use the formula:

`\[ \bar{x} \pm Z * (s)/(√(n)) \]`

Where:

`\(\bar{x}\)` is the sample mean,

s is the sample standard deviation,

n is the sample size, and

Z is the Z-score corresponding to the desired confidence level.

First, calculate the sample mean
`(\(\bar{x}\))`:

`\[ \bar{x} = (56.1 + 27 + 40.9 + 38.9 + 30.3 + 36.5 + 34.5 + 50 + 45)/(9) \]`

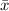`\bar{x}` ≈ 38.78

Next, find the sample standard deviation (\(s\)):

`\[ s = \sqrt{\frac{\sum_(i=1)^(9)(x_i - \bar{x})^2}{n-1}} \]`

s ≈ 9.36

Now, find the Z-score for the 80% confidence level. You can consult a standard normal distribution table or use a calculator to find Z ≈ 1.282.

Finally, substitute these values into the formula:

`\[ \text{Lower Limit} = \bar{x} - Z * (s)/(√(n)) \]`

`\[ \text{Upper Limit} = \bar{x} + Z * (s)/(√(n)) \]`

Therefore, the 80% confidence interval is approximately (32.70, 45.10). This means we can be 80% confident that the true population mean falls within this interval based on the given sample data.