Question

A rocket is launched from a tower. The height of the rocket, y in feet, is related to the time after launch, x in seconds, by the given equation. Using this equation, find the time that the rocket will hit the ground, to the nearest 100th of second.y=-16x^2+149x+108y=−16x 2 +149x+108

Answer 1

`9.99\text{secs}`

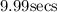
Step-by-step explanation:

Here, we want to find the time the rocket will hit the ground

What we have to do is to substitute 0 for the height of the rocket y and solve the quadratic equation that results

That simply means we are solving for:

`0=-16x^2+149x+108`

We can use the quadratic formula to solve this

`x\text{ = }\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

where a is the coefficient of x^2 which is -16

b is the coefficient of x which is 149

c is the last number which is 108

Substituting the values, we have it that:

`\begin{gathered} x\text{ = }\frac{-149\pm\sqrt[]{149^2-4(-16)(108)}}{2(-16)} \\ \\ x\text{ = }\frac{-149\pm\sqrt[]{29113}}{-32}\text{ } \\ \\ x\text{ = }\frac{-149-170.625\text{ }}{-32} \\ or\text{ } \\ x\text{ = }\frac{-149_{}+170.625}{-32} \end{gathered}`

Now, we proceed to get the individual x-values:

`\begin{gathered} x\text{ = }(-149-170.625)/(-32)\text{ = 9.99 } \\ or \\ x\text{ = }(-149+170.625)/(-32)\text{ = -0.68} \end{gathered}`

Since time cannot be negative, we use the first value only