Given that the ball travels 10 ft horizontally, then the maximum is reached at half of this distance, that is 5 ft. This means that the parabola has a maximum at (5, 25).
The equation of a parabola in vertex form is:
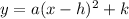
where (h, k) is the vertex.
Substituting with the vertex (5, 25) and the point (0,0) we get:
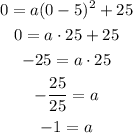
And the function that models the path traveled by the ball is:

where y is the vertical distance, or height, in ft, and x is the horizontal distance, also in ft.