Question

Daniel decided he wants to run a 5K race. He is starting by running 1 3/4 km and adding 1/2 km each day. How many days will it take him to reach his goal?

Answer 1

If he starts running 1 3/4 km the initial day, and then adding 1/2 km each day, we can model this as a linear function.

The first day he rans 1 3/4 km.

`1+(3)/(4)=(4)/(4)+(3)/(4)=(7)/(4)`

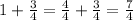
The second day he will run 1/2 km more, so this will be 1 3/4 + 1/2:

`(7)/(4)+(1)/(2)=(7)/(4)+(2)/(4)=(9)/(4)`

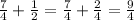
The n-th day he will run:

`(7)/(4)+(n-1)\cdot(1)/(2)=(7)/(4)+(1)/(2)n-(1)/(2)=(7)/(4)+(1)/(2)n-(2)/(4)=(5)/(4)+(1)/(2)n`

NOTE: n is the index of the day: Day 1 corresponds to n=1, Day 2 correspond to n=2 and so on.

So we have to find at which day he reaches 5 km:

`\begin{gathered} D=5=(5)/(4)+(1)/(2)n \\ 5=(5)/(4)+(2)/(4)n \\ 5\cdot4=5+2n \\ 20=5+2n \\ 20-5=2n \\ 15=2n \\ n=(15)/(2) \\ n=7.5\approx8\longrightarrow\text{ Day 8} \end{gathered}`

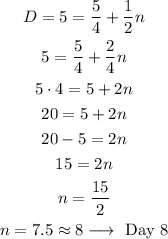
Answer: he will reach the goal at Day 8.