Question

Calculate the length of edge AD in the triangle-based pyramid below. Give your answer to 2 d.p.

Answer 1

Check the picture below.

`\tan(37^o )=\cfrac{\stackrel{opposite}{49}}{\underset{adjacent}{DB}} \implies DB\tan(37^o)=49\implies DB=\cfrac{49}{\tan(37^o)} \\\\[-0.35em] ~\dotfill\\\\ \sin( 56^o )=\cfrac{\stackrel{opposite}{DB}}{\underset{hypotenuse}{AD}} \implies AD\sin( 56^o )=DB\implies AD=\cfrac{DB}{\sin( 56^o )} \\\\\\ AD=\cfrac{ ~~ (49)/(\tan(37^o)) ~~ }{\sin( 56^o )}\implies AD=\cfrac{49}{\sin( 56^o )\tan(37^o)}\implies AD\approx 78.43~cm`

Make sure your calculator is in Degree mode.

Answer 2

`AD=78.43\; \sf cm\; (2\;d.p.)`

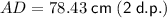
Explanation:

To calculate the length of edge AD in the given triangular-based pyramid, we first need to calculate the length of one of the legs of right triangle ABD.

From observation of the diagram, right triangle BCD and right triangle ABD both share leg BD. Therefore, we can calculate the length of BD using the tangent trigonometric ratio with ΔBCD.

`\boxed{\begin{array}{l}\underline{\textsf{Tangent trigonometric ratio}}\\\\\sf \tan(\theta)=(O)/(A)\\\\\textsf{where:}\\\phantom{ww}\bullet\;\textsf{$\theta$ is the angle.}\\\phantom{ww}\bullet\;\textsf{$O$ is the side opposite the angle.}\\\phantom{ww}\bullet\;\textsf{$A$ is the side adjacent the angle.}\end{array}}`

In triangle BCD:

• θ = ∠D = 37°
• O = BC = 49 cm
• A = BD

Substitute these values into the tangent ratio and solve for BD:

`\tan(37^(\circ))=(49)/(BD)`

`BD=(49)/(\tan(37^(\circ)))`

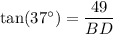
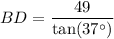
Now we have the exact length of BD, we can use the sine trigonometric ratio to find the length of AD.

`\boxed{\begin{array}{l}\underline{\textsf{Sine trigonometric ratio}}\\\\\sf \sin(\theta)=(O)/(H)\\\\\textsf{where:}\\\phantom{ww}\bullet\;\textsf{$\theta$ is the angle.}\\\phantom{ww}\bullet\;\textsf{O is the side opposite the angle.}\\\phantom{ww}\bullet\;\textsf{H is the hypotenuse (the side opposite the right angle).}\end{array}}`

In triangle ABD:

• θ = ∠A = 56°
• O = BD = 49 / tan(37°)
• H = AD

Substitute these values into the sine ratio and solve for AD:

`\sin(56^(\circ))=((49)/(\tan(37^(\circ))))/(AD)`

`AD=((49)/(\tan(37^(\circ))))/(\sin(56^(\circ)))`

`AD=(49)/(\tan(37^(\circ))\sin(56^(\circ)))`

`AD=78.4345588...`

`AD=78.43\; \sf cm\; (2\;d.p.)`

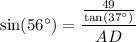
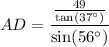
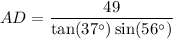
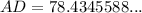
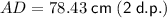
Therefore, the length of edge AD is 78.43 cm, rounded to two decimal places.