We are given the following two equations
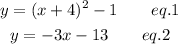
Since both equations are equal to y then we can equate them as
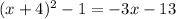
Now let us simplify the equation
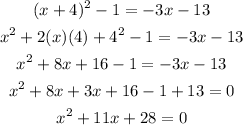
As you can see, we are left with a quadratic equation.
The standard form of a quadratic equation is given by
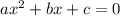
Comparing the equation with the standard form, the coefficients are
a = 1
b = 11
c = 28
Now recall that the quadratic formula is given by
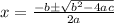
Substitute the values into the above quadratic formula
![x=\frac{-11\pm\sqrt[]{(11)^2-4(1)(28)}}{2(1)}=\frac{-11\pm\sqrt[]{121^{}-112}}{2}=\frac{-11\pm\sqrt[]{9}}{2}=(-11\pm3)/(2)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/quytepoeamd9f4bsg4z2.png)
So the two possible solutions are
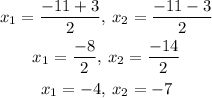
Therefore, the solutions of the equations are
x = -4 and x = -7