Given:
The wavelength of the microwave is
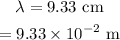
The width of the window is,
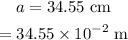
The distance between the wall from the window is,
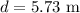
To find:
the distance from the central maximum to the first order minimum
Step-by-step explanation:
For destructive interference,
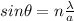
Here, for the first order, minima n=1.
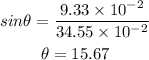
The distance from the central maximum to the first order minimum is
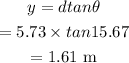
Hence, the required distance is 1.61 m.