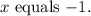Answer:
content loaded
If 3 to the power of -3x + 6 equals 27 to the power of x + 4, then x equals _-1_ .
Explanation:
Let's solve the equation:
![\[3^(-3x + 6) = 27^(x + 4)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vn2va7j3j3n4o89ao3t07oss9du4dgdnp2.png)
First, express 27 as a power of 3, since both sides of the equation should have the same base:
![\[27 = 3^3\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8o4pca0r0ktnv8yyybxpl5cyfqmczpfh8o.png)
Now substitute this into the equation:
![\[3^(-3x + 6) = (3^3)^(x + 4)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ubnvvubdtp6lfjb9h04g1lvfuijfn0hrza.png)
Use the property
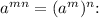
![\[3^(-3x + 6) = 3^(3(x + 4))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/48q3l6428i4qqowyfpwer94rn15hd422no.png)
Now, set the exponents equal to each other:
![\[-3x + 6 = 3(x + 4)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/umhqqmz3c7homq165h0imtfhmnw3tstx1u.png)
Expand and solve for x:
![\[-3x + 6 = 3x + 12\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/fgysytf89gqstkf9bm7fk0pwco9o89e7hy.png)
Combine like terms:
![\[6 = 6x + 12\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/us0pd50we5yoxovg7afj3vlshyu5koxwr0.png)
Subtract 12 from both sides:
![\[-6 = 6x\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xlwckccovc5gzy8gd75a0tar8ed391y04y.png)
Divide by 6:
![\[x = -1\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qguos0jrru14uflw92nm24952p2xv8n7a6.png)
Therefore,