Question

Let f(x) = e^(-1/2(x^2)) Which table describes the concavity of f?

Answer 1

Concave Up: x<-1 and x>1

Concave Down: -1<x<1

Explanation:

To determine the intervals of concavity for a continuous function f, we must determine the second derivative and figure out at what points its sign changes (aka. our inflection points):

`f(x)=e^{-(1)/(2)x^2}\\\\f'(x)=(d)/(dx)(-(1)/(2)x^2)*e^{-(1)/(2)x^2}\\\\f'(x)=-xe^{-(1)/(2)x^2}\\\\f''(x)=[(d)/(dx)(-x)](e^{-(1)/(2)x^2})+(-x)((d)/(dx)e^{-(1)/(2)x^2})\\ \\f''(x)=-e^{-(1)/(2)x^2}+x^2e^{-(1)/(2)x^2}\\\\f''(x)=e^{-(1)/(2)x^2}(x^2-1)`

Next, we determine where
`f''(x)=0` to find our inflection points:

`0=-e^{-(1)/(2)x^2}(x^2-1)\\\\x=-1,x=1`

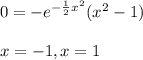
Our intervals of concavity can be determined by testing points around our inflection points. I will use the points
`x=-2` and
`x=2`:

`f''(-2)=e^{-(1)/(2)(-2)^2}((-2)^2-1)=e^(-2)(4-1)=(3)/(e^2)>0\\ \\\\f''(2)=e^{-(1)/(2)(2)^2}(2^2-1)=e^(-2)(4-1)=(3)/(e^2)>0`

Since the factor
`x^2-1` is a second-order polynomial with a leading positive coefficient, we know that the sign is negative in the interval between the roots, and positive outside. Therefore:

Concave Downward:
`(-\infty,-1) \cup(1,\infty)`

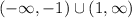
Concave Upward:
`(-1,1)`

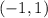
This means that the 4th option is correct. Refer to the graph for a visual.