Question

Question 1 of 10Classify the following triangle. Check all that apply.

Answer 1

Given:

We get a=6, b=11.9, and c=7, and angle B is 132 degrees.

Required:

We need to classify the given triangle.

Step-by-step explanation:

Consider the cosine law.

`cosA=(b^2+c^2-a^2)/(2bc)`

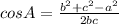
Substitute a=6, b=11.9, and c=7 in the formula.

`cosA=(11.9^2+7^2-6^2)/(2*11.9*7)`
`cosA=(154.61)/(166.6)\frac{}{}`
`cosA=0.92803121248`
`A=cos^(-1)(0.92803121248)`
`A=21.87\degree`

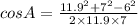
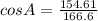
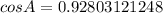
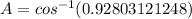
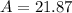
Recall that an obtuse angle is an angle greater than 90°.

The given triangle has an obtuse angle at B.

The given triangle is Obtuse.

Recall that an isosceles triangle is a triangle with (at least) two equal sides.

The given triangle has three different sides.

The given triangle is not an isosceles triangle.

Recall that a scalene triangle is a triangle in which all three sides are in different lengths, and all three angles are of different measures.

The given triangle is a scalene triangle.

Recall that an acute-angled triangle is a type of triangle in which all the three internal angles of the triangle are acute,

There is an obtuse angle.

The given triangle is not an acute triangle.

Recall that a right-angled triangle is a triangle, that has one of its interior angles equal to 90 degrees.

There is no 90 degrees angle.

The given triangle is not a right-angled triangle.

Recall that an equilateral triangle is a triangle with all three sides of equal length.

The given triangle is not an equilateral triangle since there are all three sides of different lengths.

Final answer:

Obtuse, Scalene