Question

A random sample of 36 tourists in the grand bahamas showed that they spent an average of 1,750 (in a week) with a standard deviation of 125; and a sample of 25 tourists in new province showed that they spent an average of 1,900 (in a week) with a standard deviation of 130. at 5?

Answer 1

There is sufficient evidence to suggest that there is a significant difference in the mean spending of tourists between the Grand Bahamas and New Providence at a significance level of α = 0.05.

Step-by-step explanation:

To test whether there is a significant difference in the mean spending of tourists in the Grand Bahamas and New Providence, we can use a two-sample t-test.

The null hypothesis (H0) is that there is no difference in the mean spending between the two locations, while the alternative hypothesis (H1) is that there is a significant difference.

The formula for the two-sample t-test is:

`t = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{\sqrt{(s_1^2)/(n_1) + (s_2^2)/(n_2)}}`

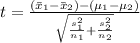
Where:

`( \bar{x}_1 )` and
`( \bar{x}_2 )`are the sample means

`( \mu_1 )` and
`( \mu_2 )` are the population means

`( s_1 )` and
`( s_2 )` are the sample standard deviations

`( n_1 )` and
`( n_2 )` are the sample sizes

Given:

Sample 1 (Grand Bahamas):

Sample mean
`(( \bar{x}_1 )) = $1,750`

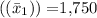
Standard deviation
`(( s_1 )) = $125`

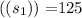
Sample size
`(( n_1 )) = 36`

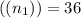
Sample 2 (New Providence):

Sample mean
`(( \bar{x}_2 )) = $1,900`

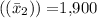
Standard deviation
`(( s_2 )) = $130`

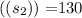
Sample size
`(( n_2 )) = 25`

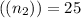
We can now calculate the t-statistic using these values.

First, let’s calculate the pooled standard deviation:

`[ s_p = \sqrt{((n_1 - 1)s_1^2 + (n_2 - 1)s_2^2)/(n_1 + n_2 - 2)}]`

Substitute the given values:

`[ s_p = \sqrt{((36 - 1)(125)^2 + (25 - 1)(130)^2)/(36 + 25 - 2)}]`

`[ s_p = \sqrt{((35)(15625) + (24)(16900))/(59)}]`

`[ s_p = \sqrt{(546875 + 405600)/(59)}]`

`[ s_p = \sqrt{(952475)/(59)}]`

`[ s_p = 163.34]`

Now, we can calculate the t-statistic:

`[ t = \frac{(1750 - 1900) - 0}{\sqrt{(125^2)/(36) + (130^2)/(25)}}]`

`[ t = \frac{-150}{\sqrt{(15625)/(36) + (16900)/(25)}}]`

`[ t ≈ -150 / (23.15)]`

`[ t = -6.48]`

Using a significance level of α = 0.05, with degrees of freedom

`df = ( n_1 + n_2 - 2 = 36 + 25 - 2 = 59)`

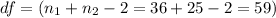
we can compare the calculated t-statistic to the critical t-value from a t-distribution table.

If the calculated t-statistic falls in the rejection region, we reject the null hypothesis.

The critical t-value for a two-tailed test with α = 0.05 and df = 59 is approximately ±2.000.

Since our calculated t-statistic (-6.48) falls in the rejection region (outside of ±2.000), we reject the null hypothesis.