Question

X - 1/2 = 3/4 what is the answer I don’t have a clue

Answer 1

`{ \boxed{ \: x = (5)/(4) \: }}`

Explanation:

`x - (1)/(2) = (3)/(4) \\`

• To make x the subject, let's add ½ on both sides;

`(x - (1)/(2) ) + (1)/(2) = ( (3)/(4) ) + (1)/(2) \\ \\ x = (3)/(4) + (1)/(2)`

• To solve the operation above, the LCM of 4 and 2 is 4. From the formula below;

`{ \boxed{ \tt{ \red{( x )/(a) + (y)/(b) = \frac{ \{(lcm / a) * x \} + \{(lcm / b) * y \}}{lcm = (ab)} }}}}`

Therefore;

`x = \frac{ \{(4 / 4) * 3 \}+ \{(4 / 2) * 1 \} }{4} \\ \\ x = (3 + 2)/(4) \\ \\ x = (5)/(4)`

Answer 2

`\sf x = (5)/(4)`

Explanation:

`\sf x - (1)/(2) = (3)/(4)`

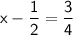
To isolate the variable
`\sf x`, we can add
`\sf (1)/(2)` to both sides of the equation:

`\sf x - (1)/(2) + (1)/(2) = (3)/(4) + (1)/(2)`

On the left side, the
`\sf (1)/(2)` terms cancel out, leaving:

`\sf x = (3)/(4) + (1)/(2)`

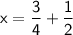
Now, find a common denominator to add the fractions on the right side. The common denominator for 4 and 2 is 4. So, rewrite
`\sf (1)/(2)` with the denominator 4:

`\sf x = (3)/(4) + (2)/(4)`

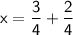
Now, add the numerators:

`\sf x = (3+2)/(4)`

`\sf x = (5)/(4)`

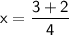
So, the solution to the equation
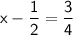`\sf x - (1)/(2) = (3)/(4)` is
`\sf x = (5)/(4)`.