Question

Is the function even,odd, or neither

Answer 1

even I think

Explanation:

Answer 2

Neither

Explanation:

If f (–x) = f (x), then the function is even. if f (–x) = –f (x), (all the signs are flipped) the it is odd.

To apply this to the function here, simply replace the x in
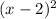`(x-2)^(2)` with -x.

`(x-2)^(2)` =
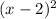`x^(2)` - 4x + 4, and
`(-x - 2)^(2)` =
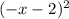`x^(2)` +4x + 4.

Since
`x^(2)`+4x + 4 doesnt equal
`x^(2)` - 4x + 4 (even) or
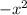`-x^(2)`+4x -4 (odd), the function is neither even nor odd.