Question

Please help me solve the following problem:Mary has a box with the shape of a semisphere where she keeps cheese. Inside the box there is a cubic cheese with 10 cm edge. The four top vertices of the cheese are in contact withthe cover of the box (see image).Which is the volume of the box?

Answer 1

`Volume\text{ of the box = 3847.60 cm}^3`

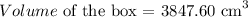
Step-by-step explanation:

Given:

The box is in the shape of a semisphere

The edge of the cubic cheese = 10cm

To find:

the volume of the box

The box is said to be a semisphere. This is also known as the hemisphere.

To get the volume of the box, we will apply the volume of a hemisphere.

The volume is given as:

`Volume\text{ of a hemisphere = }(2)/(3)\pi r^3`

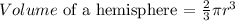
The 4 top vertices start from the cover of the box (hemisphere).

From the diagram, radius = AC

AB is an edge = 10

We need to get the distance BD using pythagoras theorem:

Hypotenuse² = opposite² + adjacent²

opposite = 10, adjacent = 10

BD² = 10² + 10²

BD² = 200

BD = √200 = √(100×2)

BD = 10√2

Next, we will find BC:

BD = BC + CD

BC = CD

BD = 2BC

BC = BD/2

BC = (10√2)/2

To get the radius, we will use Pythagoras theorem on triangle ABC

AB = opposite = 10

BC = adjacent = (10√2)/2

AC = hypotenuse = radius

Substitute the values into the Pythagoras formula:

`\begin{gathered} Volume\text{ of a hemisphere = }(2)/(3)\pi r^3 \\ \\ let\text{ }\pi\text{ = the value on a calculator} \\ r\text{ = 12.2474} \\ \\ Volume\text{ of the hemisphere = }(2)/(3)*\pi*(12.2474)^3 \\ \\ Volume\text{ of the hemisphere = 3847.60 cm}^3 \\ \\ Volume\text{ of the box= 3847.60 cm}^3 \end{gathered}`