Question

A torque of 37.1 N · m is applied to an initially motionless wheel which rotates around a fixed axis. This torque is the result of a directed force combined with a friction force. As a result of the applied torque the angular speed of the wheel increases from 0 to 10.5 rad/s. After 5.90 s the directed force is removed, and the wheel comes to rest 59.0 s later.

(a) What is the wheel's moment of inertia (in kg · m2)?
(b) What is the magnitude of the torque caused by friction (in N · m)?
(c) From the time the directed force is initially applied, how many revolutions does the wheel go through?

Answer 1

a. The moment of inertia of the wheel is approximately
`\( 20.8 \, \text{kg}\cdot\text{m}^2 \).`

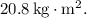
b. The magnitude of the torque caused by friction is approximately \
`( 37.1 \, \text{N}\cdot\text{m} \).`

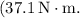
c. The wheel goes through approximately 48.6 revolutions.

How did we get the values?

(a) The angular acceleration (α) can be calculated using the formula:

`\[ \alpha = (\Delta \omega)/(\Delta t) \]`

where
`\( \Delta \omega \)` is the change in angular velocity and
`\( \Delta t \)` is the time over which the change occurs. In this case,

`\[ \alpha = \frac{10.5 \, \text{rad/s} - 0}{5.90 \, \text{s}} \]`

`\[ \alpha = 1.779 \, \text{rad/s}^2 \]`

Now, the torque
`(\( \tau \))` can be related to angular acceleration and moment of inertia
`(\( I \))` by the equation:

`\[ \tau = I \cdot \alpha \]`

Solving for
`\( I \)`:

`\[ I = (\tau)/(\alpha) \]`

Substituting the given values:

`\[ I = \frac{37.1 \, \text{N}\cdot\text{m}}{1.779 \, \text{rad/s}^2} \]`

`\[ I \approx 20.8 \, \text{kg}\cdot\text{m}^2 \]`

So, the moment of inertia of the wheel is approximately
`\( 20.8 \, \text{kg}\cdot\text{m}^2 \).`

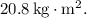
(b) After the directed force is removed, the only torque acting on the wheel is due to friction. The torque caused by friction
`(\( \tau_{\text{friction}} \))` can be calculated using the equation:

`\[ \tau_{\text{friction}} = I \cdot \alpha \]`

where
`\( \alpha \)` is the angular acceleration during the deceleration phase. Since the wheel comes to rest,
`\( \alpha \)` is the angular acceleration when the angular velocity becomes zero. This is the negative of the previous angular acceleration:

`\[ \alpha_{\text{friction}} = -1.779 \, \text{rad/s}^2 \]`

`\[ \tau_{\text{friction}} = 20.8 \, \text{kg}\cdot\text{m}^2 \cdot (-1.779 \, \text{rad/s}^2) \]`

`\[ \tau_{\text{friction}} \approx -37.1 \, \text{N}\cdot\text{m} \]`

So, the magnitude of the torque caused by friction is approximately
`\( 37.1 \, \text{N}\cdot\text{m} \).`

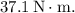
(c) To find the number of revolutions, we need to use the relationship between angular displacement
`(\( \theta \))`, angular velocity
`(\( \omega \))`, and time
`(\( t \))`:

`\[ \theta = \omega_{\text{avg}} \cdot t \]`

where
`\( \omega_{\text{avg}} \)` is the average angular velocity during the period. In this case,
`\( \omega_{\text{avg}} \)` can be approximated as the initial angular velocity
`(\( \omega_0 \))`plus the final angular velocity
`(\( \omega_f \))` divided by 2:

`\[ \omega_{\text{avg}} = (\omega_0 + \omega_f)/(2) \]`

`\[ \omega_{\text{avg}} = \frac{0 + 10.5 \, \text{rad/s}}{2} = 5.25 \, \text{rad/s} \]`

Now, substituting into the angular displacement formula:

`\[ \theta = 5.25 \, \text{rad/s} \cdot (59.0 \, \text{s} - 5.90 \, \text{s}) \]`

`\[ \theta \approx 305.25 \, \text{rad} \]`

Finally, to convert radians to revolutions, use the fact that
`\( 2\pi \)` radians is one revolution:

`\[ \text{Number of revolutions} = \frac{305.25 \, \text{rad}}{2\pi} \]`

`\[ \text{Number of revolutions} \approx 48.6 \]`

So, the wheel goes through approximately 48.6 revolutions.