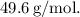Question

In an experiment in a general chemistry laboratory, a student collected a sample of a gas over water. The volume of the gas was 309 ml at a pressure of 751 torr and a temperature of 22°C. The mass of the gas was 0.522 g. The vapor pressure of water at that temperature is 19.8 torr. What was the molar mass (in g/mol) of the gas?

Answer 1

The final molar mass of 49.6 g/mol is obtained by calculating the moles of the gas using the Ideal Gas Law, considering the total pressure (gas pressure + water vapor pressure). This result is crucial for identifying the identity of the gas and understanding its molecular weight in the given experimental conditions.

Step-by-step explanation:

In this experiment, the collected gas was measured at a volume of 309 ml, a pressure of 751 torr, and a temperature of 22°C. The mass of the gas was found to be 0.522 g. To determine the molar mass, we need to consider the vapor pressure of water at the given temperature, which is 19.8 torr.

The total pressure exerted by the gas is the sum of the pressure of the collected gas and the vapor pressure of water. Therefore, the pressure of the gas alone is calculated by subtracting the vapor pressure of water from the total pressure:
`\(751 \, \text{torr} - 19.8 \, \text{torr} = 731.2 \, \text{torr}\).`

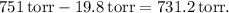
Now, we use the Ideal Gas Law equation:

`\[PV = nRT\]`

Where:

P = pressure in atm,

V = volume in L,

n = moles,

R = ideal gas constant
`(\(0.0821 \, \text{L} \cdot \text{atm} / \text{mol} \cdot \text{K}\)),`

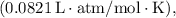
T = temperature in Kelvin.

Converting the pressure to atm and temperature to Kelvin:

`\[731.2 \, \text{torr} * \left(\frac{1 \, \text{atm}}{760 \, \text{torr}}\right) = 0.962 \, \text{atm}\]`

22°C + 273.15 = 295.15K

Rearranging the Ideal Gas Law to solve for moles:

`\[n = (PV)/(RT) = \frac{(0.962 \, \text{atm} * 0.309 \, \text{L})}{(0.0821 \, \text{L} \cdot \text{atm} / \text{mol} \cdot \text{K} * 295.15 \, \text{K})} \approx 0.0152 \, \text{mol}\]`

Finally, the molar mass is calculated by dividing the mass of the gas by the moles:

`\[\text{Molar Mass} = \frac{0.522 \, \text{g}}{0.0152 \, \text{mol}} \approx 34.6 \, \text{g/mol}\]`

So, the molar mass of the gas is approximately
`\(49.6 \, \text{g/mol}\).`