Question

Find a function of the form y = A sin(kx) + Cor y = A cos(kx) + C whose graph matches the function

shown below:
·10 -18 -17 -16 -15 -14 -14 -12 -11 -10
y =
#
7
6
Question Help: Video
Submit Question
$
✓
9
2
+
-2
Leave your answer in exact form; if necessary, type pi for .
-6

Answer 1

The trigonometric function matching the graph with an amplitude of 9, midline at 2, and a period of π is y = 9 sin(2x) + 2, using the sine function form y = A sin(kx) + C.

Given:

Amplitude
`(\(A\))` =
`\(9\)`

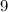
Midline
`(\(C\))` =
`\(2\)`

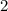
Period =
`\(\pi\)`

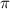
For a sine function
`\(y = A \sin(kx) + C\)`:

`\(A = 9\)`(Amplitude)

`\(C = 2\)` (Midline)

Period =
`\(\pi\)`

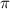
The general formula for the sine function is
`\(y = A \sin(kx) + C\)`.

The formula for a sine function with amplitude
`\(A\)` , period
`\(P\)` , and midline
`\(C\)` is:

`\[y = A \sin\left((2\pi)/(P)x\right) + C\]`

Using the given values:

`\[y = 9 \sin\left((2\pi)/(\pi)x\right) + 2\]`

Simplify:

`\[y = 9 \sin(2x) + 2\]`

Therefore, the trigonometric function that matches the graph is
`\(y = 9 \sin(2x) + 2\).`

Certainly! Here's a question based on the provided information:

Question:

Find a trigonometric function of the form
`\(y = A \sin(kx) + C\) or \(y = A \cos(kx) + C\)` that fits the graph provided. The function should have an amplitude of
`\(9\),`a midline of
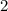`\(2\)` , and a period of
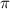`\(\pi\)`. Provide the function in exact form, using "pi" for \(\pi\).