H= 20°
Step-by-step explanation
as HJ is congruent to HK , here we have an isosceles triangle, The angles opposite to equal sides are equal in measure,so
Step 1
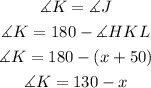
also, we know the sum of the internal angles in a triangle equals 180, so
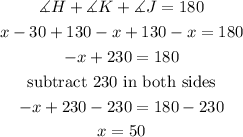
Step 2
now, replace in angle H

therefore, the measurement fo H is
H= 20°
I hope this helps you