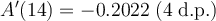Question

Shown below in these images are my calculus questions. Any help you give is much appreciated, I'm trying to catch up for end of term, Thank you!!

Answer 1

`\textsf{1)} \quad f'(x)=\left((x^9(x-6)^3)/((x^2+8)^7)\right)\left((9)/(x)+(3)/(x-6)-(14x)/(x^2+8)\right)`

`\begin{aligned}\textsf{2)}\quad &P(t)=510000(1.052)^t\\&P'(t)=510000 (1.052^t)\ln(1.052)\\&P'(25)=91815\end{aligned}`

`\begin{aligned}\textsf{3)}\quad &A(t)=8e^{-(t\ln(2))/(13)}\\&A'(t)=-\frac{8\ln(2)e^{-(t\ln(2))/(13)}}{13}\\&A'(14)=-0.2022\end{aligned}`

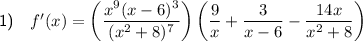
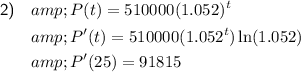
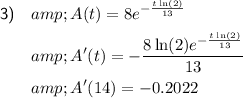
Explanation:

Question 1

Given:

`f(x)=(x^9(x-6)^3)/((x^2+8)^7)`

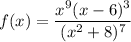
To find the derivative of the given function f(x) using logarithmic differentiation, begin by taking the natural logarithm (ln) of both sides of the equation:

`\ln(f(x)) = \ln\left((x^9(x-6)^3)/((x^2+8)^7)\right)`

Use logarithmic properties to simplify the right side:

`\ln(f(x))=\ln (x^9(x-6)^3)-\ln((x^2+8)^7)`

`\ln(f(x))=\ln (x^9)+\ln((x-6)^3)-\ln((x^2+8)^7)`

`\ln(f(x))=9\ln (x)+3\ln(x-6)-7\ln(x^2+8)`

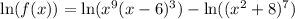
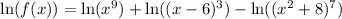
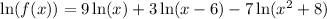
Now, differentiate both sides with respect to x using the following rule:

`\boxed{\begin{array}{c} \underline{\textsf{Differentiating $\ln(f(x))$}}\\\\(d)/(dx)\left(\ln(f(x))\right)=(f'(x))/(f(x))\end{array}}`

Therefore:

`(f'(x))/(f(x))=(9)/(x)+(3)/(x-6)-(14x)/(x^2+8)`

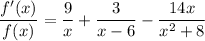
Solve for f'(x):

`f'(x)=f(x)\left((9)/(x)+(3)/(x-6)-(14x)/(x^2+8)\right)`

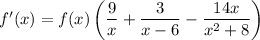
Substitute in f(x):

`f'(x)=\left((x^9(x-6)^3)/((x^2+8)^7)\right)\left((9)/(x)+(3)/(x-6)-(14x)/(x^2+8)\right)`

`\hrulefill`

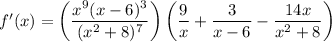
Question 2

The general formula for population growth is given by:

`P(t) = P_0(1+r)^t`

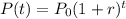
where:

• P(t) is the population at time (t).
• P₀ is the initial population.
• r is the growth rate (expressed as a decimal).
• t is the time in years.

In this case:

• P₀ = 510000
• r = 5.2% = 0.052
• t is the number of years since the year 2000.

Therefore, the exponential function that relates the total population, P(t), as a function of t, the number of years since 2000 is:

`P(t)=510000(1.052)^t`

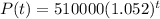
To find the rate at which the population is increasing, we need to find the derivative of P(t) with respect to t.

`\boxed{\begin{array}{c} \underline{\textsf{Differentiating $a^x$}}\\\\(d)/(dx)\left(a^x\right)=a^x \ln (a)\\\\\textsf{for any constant $a$}\end{array}}`

Therefore:

`P'(t)=510000 \cdot 1.052^t \cdot \ln(1.052)`

`P'(t)=510000 (1.052^t)\ln(1.052)`

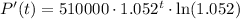
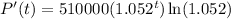
To determine the rate of population increase in the year 2025, substitute t = 25 into the expression for P'(t):

`P'(25)=510000 (1.052^(25))\ln(1.052)`

`P'(25)=91814.7898090...`

`P'(25)=91815`

`\hrulefill`

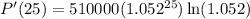
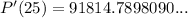
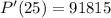
Question 3

The formula for the half-life of a substance is:

`\large\text{$A(t)=A_0e^(kt)$}`

where:

• A(t) is the quantity of the substance remaining.
• A₀ is the initial quantity of the substance.
• t is the time elapsed.
• k is the decay constant.

As the initial quantity of the isotope is 8 g, substitute A₀ = 8 into the formula:

`A(t)=8e^(kt)`

As the half-life is 13 hours, then A(t) = 4 when t = 13.

Therefore, to find the value of k, substitute t = 13 and A(t) = 4 into the equation and solve for k:

`4=8e^(13k)`

`(1)/(2)=e^(13k)`

`\ln\left((1)/(2)\right)=\ln\left(e^(13k)\right)`

`\ln(1)-\ln(2)=13k`

`k=-(\ln(2))/(13)`

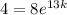
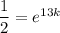
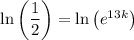
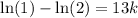
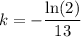
Therefore, the exponential function that relates the amount of substance remaining is:

`\large\text{$A(t)=8e^{-(t\ln(2))/(13)}$}`

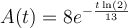
where A(t) is the number of grams of isotope remaining, and t is the time in hours.

To determine the rate at which the substance is decaying after t hours, we can take the derivative of A(t) with respect to t:

`\boxed{\begin{array}{c} \underline{\textsf{Differentiating $e^(f(x))$}}\\\\(d)/(dx)\left(e^(f(x))\right)=f'(x)\cdot e^(f(x))\end{array}}`

`f(t)=-(t\ln(2))/(13) \implies f'(t)=-(\ln(2))/(13)`

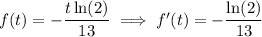
Therefore:

`\large\text{$A'(t)=-(\ln(2))/(13)\cdot 8 \cdot e^{-(t\ln(2))/(13)}$}`

`\large\text{$A'(t)=-\frac{8\ln(2)e^{-(t\ln(2))/(13)}}{13}$}`

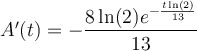
To determine the rate of decay at 14 hours, substitute t = 14 into A'(t):

`\large\text{$A'(14)=-\frac{8\ln(2)e^{-(14\ln(2))/(13)}}{13}$}`

`\large\text{$A'(14)=-0.2022$\;(4\;d.p.)}`