Question

Tarzan plans to cross a gorge by swinging in an arc from a hanging vine as shown. If he swings across the gorge at 5 m/s and his mass is 78 kg and the vine is 5.2 m long, what is the tension in the vine at the lowest point?

1) less than 780N
2) 780N
3) more than 780N

Answer 1

To find the tension in the vine at the lowest point, we can consider the forces acting on Tarzan at that moment. The tension in the vine at the lowest point is equal to the centripetal force, which is approximately 750 N. Therefore, the correct answer is less than 780N (Option 1).

Step-by-step explanation:

To find the tension in the vine at the lowest point, we can consider the forces acting on Tarzan at that moment. At the lowest point of the swing, the tension in the vine provides the centripetal force necessary to keep Tarzan moving in a circular path.

The centripetal force (Fc) can be calculated using the formula:

Fc =
`(m \cdot v^2)/(r)`

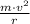
where:

- m is the mass of Tarzan (78 kg),

- v is the velocity of Tarzan (5 m/s),

- r is the radius of the circular path (half of the length of the vine,
`\( (5.2)/(2) \)` m).

Fc =
`\frac{78 \, \text{kg} \cdot (5 \, \text{m/s})^2}{(5.2)/(2) \, \text{m}}`

Fc ≈
`\frac{78 \, \text{kg} \cdot 25 \, \text{m/s}^2}{2.6 \, \text{m}}`

Fc ≈
`\frac{1950\, \text{N} }{2.6}`

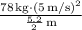
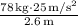
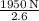
Fc ≈ 750 N

The tension in the vine at the lowest point is equal to the centripetal force, which is approximately 750 N. Therefore, the correct answer is less than 780N (Option 1).