Since we don't know the height of the flagpole, we will asign a variable "h" to represent it. We can create a proportion between the two objects and their shadows, this is done by using fractions. One fraction will have the height of the flagpole over the size of its shadow, then we equate it with the other fraction that has the height of the tree, over the length of its shadow. Then we solve for the unkown variable. This is done below:
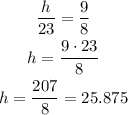
The height of the flagpole is approximately 25.9 feet