Question

The radius of a circle is decreasing at a constant rate of 2 meters per second. At the instant when the area of the circle is 49π square meters, what is the rate of change of the area? Round your answer to three decimal places.

Answer 1

dA/dt = -87.965 m²/s; the negative indicates the area is decreasing, your instructor may want the magnitude of this answer.

Explanation:

Given:

• dr/dt = - 2 m/s ("-" because "decreasing")

Find:

• dA/dt when A = 49π m²

To find the rate of change of the area of the circle, we can use calculus, specifically the concept of related rates. Here's how we can approach this problem:

We know the area of a circle is given as:

`\Longrightarrow A = \pi r^2`

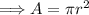
Where,

• 'A' is the area of the circle
• 'π' is a mathematical constant
• 'r' is the radius of the circle

From Leibniz version of the chain rule, we have:

`\displaystyle \Longrightarrow (dA)/(dt)=(dA)/(dr)(dr)/(dt)`

Where,

• 'dA/dt' is the rate the area changes due to time
• 'dA/dr' is the rate the area changes due to the radius
• 'dr/dt' is the rate the radius changes due to time

Let's plug in what we know:

`\displaystyle \Longrightarrow (dA)/(dt)=(d)/(dr)\left[\pi r^2\right](-2)\\\\\\\\ \Longrightarrow (dA)/(dt)=\pi(d)/(dr)\left[ r^2\right](-2)\\\\\\\\ \Longrightarrow (dA)/(dt)=2\pi r(-2)\\\\\\\\\therefore (dA)/(dt)=-4\pi r`

When A = 49π m² the radius is found by:

`\Longrightarrow A = \pi r^2\\\\\\\\\Longrightarrow 49 \pi = \pi r^2\\\\\\\\\Longrightarrow 49 = r^2\\\\\\\\\Longrightarrow r = √(49)\\\\\\\\\therefore r = 7 \ m`

Now using the formula we derived earlier, we can find the rate of change of the area when the radius is 7 meters:

`\displaystyle \Longrightarrow (dA)/(dt)=-4\pi r\\\\\\\\ \Longrightarrow (dA)/(dt)=-4\pi (7 \ m)\\\\\\\\ (dA)/(dt)=-28 \pi \ m^2/s\\\\\\\\\therefore (dA)/(dt) \approx \boxed{-87.965 \ m^2/s}`

Thus, the rate of change of the area of the circle is approximately -87.965 m²/s rounded to 3 d.p. Note that the negative indicates the area is decreasing.