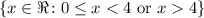Question

If f(x)=2-X^(1/2) and g(x)=x^2-9, what is the domain of g(x) divided by f(x)

Answer 1

The first step we need to take is find the expression of g(x) divided by f(x):

`h(x)=\frac{x^2-9}{2-x^{(1)/(2)}}`

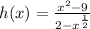
We can rewrite the fractional power as a square root.

`h(x)=\frac{x^2-9}{2-\sqrt[]{x}}`

There are two possible restrictions on this domain. The first one exists because of the square root, a square root doesn't have real results for negative values, so x can't be negative. There is a second restriction, since we have a polynomial on the denominator, we need to make sure that the values for x don't make the polynomial equal to 0, because we can't divide by 0. To find these values we must equate the expression with 0 and solve for x.

`\begin{gathered} 2-\sqrt[]{x}=0 \\ \sqrt[]{x}=2 \\ (\sqrt[]{x})^2=2^2 \\ x=4 \end{gathered}`

Therefore "x" can't be 4, nor negative. So the domain is:

`\mleft\lbrace x\in\mathfrak{\Re }\colon0\le x<4\text{ or }x>4\mright\rbrace`