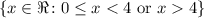The first step we need to take is find the expression of g(x) divided by f(x):
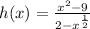
We can rewrite the fractional power as a square root.
![h(x)=\frac{x^2-9}{2-\sqrt[]{x}}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/evgs5mub0w0w3mgxdp7x.png)
There are two possible restrictions on this domain. The first one exists because of the square root, a square root doesn't have real results for negative values, so x can't be negative. There is a second restriction, since we have a polynomial on the denominator, we need to make sure that the values for x don't make the polynomial equal to 0, because we can't divide by 0. To find these values we must equate the expression with 0 and solve for x.
![\begin{gathered} 2-\sqrt[]{x}=0 \\ \sqrt[]{x}=2 \\ (\sqrt[]{x})^2=2^2 \\ x=4 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/6vmfo2dn8nhctl2jms4r.png)
Therefore "x" can't be 4, nor negative. So the domain is: