When we open the brackets of an absolute value we get the following:
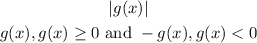
So in this case we have:

After open the absolute balue we get two expressions. The first one is:
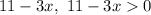
And the second one is:
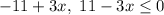
So let's work with the inequalities of each case. The one in the first case is:
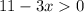
We can add 3x to both sides:
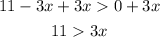
And we divide both sides by 3:
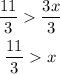
The inequality in the second case is:
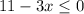
We can add 3x to both sides:

And divide by 3:

Then the two parts of the function are:

Then the answers are the second and fourth options.