Final Answer:
The tension in the string at 30° is approximately 42.3 N, and the tension in the string at 70° is approximately 38.3 N.
Step-by-step explanation:
When an object is in equilibrium, the sum of the forces acting on it is zero, and the sum of the torques (moments) is also zero. In this scenario, the object is suspended by two strings at angles of 30° and 70° to the vertical.
Firstly, resolve the weight
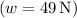 into horizontal and vertical components. The vertical component is
into horizontal and vertical components. The vertical component is
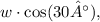 and the horizontal component is
and the horizontal component is
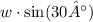 . Similarly, the vertical and horizontal components of the weight for the other string are
. Similarly, the vertical and horizontal components of the weight for the other string are
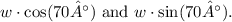
Since the object is in equilibrium, the sum of vertical forces is zero, and the sum of horizontal forces is zero. This gives two equations:
![\[ T_(30°) \cdot \cos(30°) + T_(70°) \cdot \cos(70°) = w \cdot \cos(30°) + w \cdot \cos(70°) \]](https://img.qammunity.org/2024/formulas/physics/high-school/2co90bif24pkx4sea3p85d3waryw15uuzz.png)
![\[ T_(30°) \cdot \sin(30°) - T_(70°) \cdot \sin(70°) = w \cdot \sin(30°) - w \cdot \sin(70°) \]](https://img.qammunity.org/2024/formulas/physics/high-school/tfzsu4rw9b5gprqs1iumfwd8406frzlsiz.png)
Now, solve these two equations to find the tensions
 . The solutions are
. The solutions are
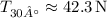 and
and
