Since she wants to obtain 150 ounces of the mixture of A and B, then
Add A and B, then equate the sum by 150
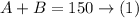
Since 40% of A is salt
Since 65% of B is salt
Since 150 ounces has 55% salt, then
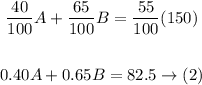
Now, we have a system of equations to solve it
Multiply equation (1) by -0.40 to make the coefficients of A equal in values and opposite in signs
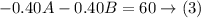
Add equations (2) and (3)
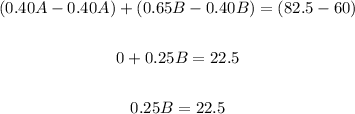
Divide both sides by 0.25
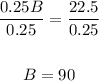
Substitute B in equation (1) by 90 to find A
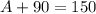
Subtract 90 from each side
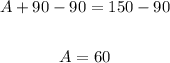
There are 60 ounces of A and 90 ounces of B