Question

A principal amount of $1,485 is placed in a savings account with an annual interest rate of 2.56% compounded monthly. How much interest does the account earn after 6 years?

Answer 1

$246.26

Explanation:

To calculate the interest earned on a principal amount compounded monthly, we can use the compound interest formula:

`\sf A = P \left(1 + (r)/(n)\right)^(nt)`

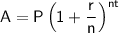
Where:

-
`\sf A` is the amount after
`\sf t` years.

-
`\sf P` is the principal amount (initial deposit).

-
`\sf r` is the annual interest rate (in decimal form).

-
`\sf n` is the number of times interest is compounded per year.

-
`\sf t` is the time the money is invested or borrowed for in years.

In this case:

-
`\sf P = \$1,485`

-
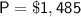
`\sf r = 2.56\%` or
`\sf 0.0256` (converted to decimal form)

-
`\sf n = 12` (compounded monthly)

-
`\sf t = 6` years

Substitute these values into the compound interest formula:

`\sf A = 1485 \left(1 + (0.0256)/(12)\right)^(12 * 6)`

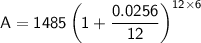
Now, calculate the final amount after 6 years:

`\sf A = 1485 \left(1 + (0.0256)/(12)\right)^(72)`

`\sf A \approx 1485 * (1+ 0.002133333333)^(72)`

`\sf A \approx 1485 * (1.002133333333)^(72)`

`\sf A \approx 1485 * 1.165833629`

`\sf A \approx 1,719.15`

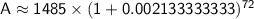
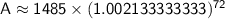
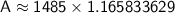
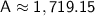
Now, calculate the interest earned:

`\sf \textsf{Interest} = A - P`

`\sf \textsf{Interest} = 1731.262939 - 1,485`

`\sf \textsf{Interest} = 246.2629393`

`\sf \textsf{Interest} = 246.26 \textsf{( in 2 d.p.)}`

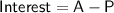
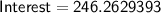
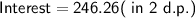
Therefore, the account earns $246.26 in interest after 6 years.