Final Answer:
The Maclaurin series for the function
 is accurately represented by the expression
is accurately represented by the expression
 making option A the correct choice. This result is obtained by substituting
making option A the correct choice. This result is obtained by substituting
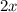 into the Taylor series expansion formula for the natural logarithm and simplifying the terms to capture the first four non-zero terms.
into the Taylor series expansion formula for the natural logarithm and simplifying the terms to capture the first four non-zero terms.
Step-by-step explanation:
Certainly! Let's find the Maclaurin series for the function
 in detail.
in detail.
The Maclaurin series for
 is given by the formula:
is given by the formula:
![\[ \ln(1 + x) = x - (x^2)/(2) + (x^3)/(3) - (x^4)/(4) + \ldots \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/y8ws7jr4j64nru1p0k9ra87jt9fdslq94g.png)
Now, substitute
 in this formula:
in this formula:
![\[ f(x) = \ln(1 + 2x) = 2x - ((2x)^2)/(2) + ((2x)^3)/(3) - ((2x)^4)/(4) + \ldots \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8kkauefp73h0ccbptbnxqo8ullv7aiaqv5.png)
Simplify each term:
![\[ = 2x - 2x^2 + (8)/(3)x^3 - (16)/(4)x^4 + \ldots \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/km13joun85bn63p0rmolsb96om3dnchc4a.png)
Therefore, the first four non-zero terms of the Maclaurin series for
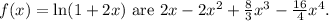
Understanding the pattern and coefficients in the Taylor series expansion of
 allows us to confidently substitute
allows us to confidently substitute
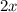 into the formula to find the Maclaurin series for
into the formula to find the Maclaurin series for
 . The calculation involves basic algebraic operations and the application of the general formula for the Maclaurin series of the natural logarithm function.
. The calculation involves basic algebraic operations and the application of the general formula for the Maclaurin series of the natural logarithm function.
So correct option is option A