Question

The absolute value function g(x) = |x − 2| − 4 is reflected over the x-axis, and then translated 2 units right and 2 units down to become g′(x). The quadratic function f(x), graphed below, is translated 2 units left and 5 units up to become f′(x). Which of these two transformed functions has a larger maximum and what is the value of this maximum?

Answer 1

The given function is

`g(x)=\lvert{x-2}\lvert-4`

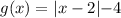
When reflected across the x-axis and translate 2 units right, and 2 units down, then its image will be

`\begin{gathered} g^(\prime)(x)=-\lvert{x-2-2}\rvert-4-2 \\ g^(\prime)(x)=-\lvert{x-4}\rvert-6 \end{gathered}`

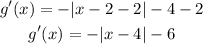
Then its maximum vertex is (4, -6)

Since the maximum value is the y-coordinate of the maximum point, then

Its maximum value is -6

From the graph, we can see that the maximum point of f(x) is (-2, -4)

Since it will translate 2 units left and 5 units up, then

Subtract 2 from the x-coordinate, and add 5 to the y-coordinate of f(x) to find the maximum point of f'(x)

`(-2+2,-4+5)=(0,1)`

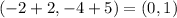
The maximum point of f'(x) is (0, 1)

The maximum value of f'(x) is 1

Since 1 > -6, then

f'(x) > g'(x)

f'(x) has a larger maximum and it is 1

The answer is C (3rd choice)