Given:
Required:
To find the total surface area of the prism.
Step-by-step explanation:
The total surface area of the prism is given by the formula:
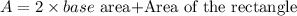
Area of the base triangle
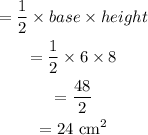
To find the width of the rectangle we will use the Pythagoras theorem.
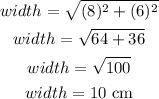
Area of the rectangle
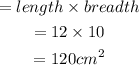
Thus the area of the prism
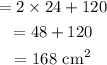
Final Answer: