Question

Mrs. Kenny is at the airport towing her 20.0 kg suitcase at constant speed by pulling a strap at an angle of 55 degrees above the horizontal. (SHOW WORK)

a. If she is pulling the suitcase at a constant speed, what is the acceleration? What is the net force?
b. If the tension force pulling on the handle is 35 N, what is the frictional force?

Answer 1

(a) Acceleration and the net force are zero.

(b) 20.1 N

Step-by-step explanation:

To address this question, we'll break it down into two parts: understanding the acceleration and net force when Mrs. Kenny is pulling the suitcase at constant speed (part a), and determining the frictional force given the tension force in the strap (part b).

`\hrulefill`

Part (a): Acceleration and Net Force
`\hrulefill`

Acceleration: When an object moves at a constant speed, its acceleration is zero. This is a fundamental principle in physics, as constant speed implies no change in velocity.

Net Force: Newton's first law of motion states that if the velocity of an object is constant (including being at rest), then the net force acting on it is zero. Since Mrs. Kenny is pulling the suitcase at a constant speed, the net force on the suitcase is zero.

`\hrulefill`

Part (b): Frictional Force
`\hrulefill`

Given:

• F = 35 N
• m = 20.0 kg
• θ = 55°

To help us answer part (b) I have attached a free-body diagram as an image attachment for you to view. We already know from part (a) that the acceleration and net force of the suitcase equal zero. Using this information along with the attached free-body diagram, let's do a sum of forces. Starting with the horizontal forces:

`\Longrightarrow \sum \vec F_x: \vec f_k \cos(180 \textdegree)+\vec F\cos(\theta)=0\\\\\\\\\Longrightarrow (35 \ N)\cos(55 \textdegree)-\vec f_k=0\\\\\\\\\Longrightarrow \vec f_k =(35 \ N)\cos(55 \textdegree)`

Note that we will not have to add up the forces acting in the vertical direction. The above calculation will give us the value of the frictional force:

`\therefore \vec f_k \approx \boxed{20.1 \ N}`

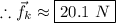
Thus, the frictional force is approximately 20.1 N.