Question

9. Select values of an exponential function are given in the table. X -2 0 4 5

Answer 1

The form of the exponential function is

`y=a(b)^x`

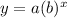
Where a is the value of y at x = 0

b is the base of the exponential function

Let us use 2 points from the table to find a and b

∵ At x = 0, y = 4

∵ a is the value of y at x = 0

∴ a = 4

Substitute it in the form of the function

`f(x)=4(b)^x`

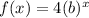
Now let us use the point (-1, 4/3)

`\because f(-1)=(4)/(3);x=-1\text{and y = }(4)/(3)`
`(4)/(3)=4(b)^(-1)`

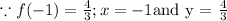
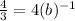
Divide both sides by 4

`\begin{gathered} ((4)/(3))/(4)=(4b^(-1))/(4) \\ (1)/(3)=b^(-1) \end{gathered}`

To change the power of b to +1, reciprocal 1/3

`\begin{gathered} \because(1)/(3)=(1)/(b) \\ \therefore b=3 \end{gathered}`

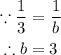
The function of the table is

`f(x)=4(3)^x`

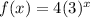
The answer is D