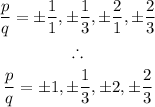DEFINITIONS
The Rational Roots Test (also known as Rational Zeros Theorem) allows us to find all possible rational roots of a polynomial. Suppose we have some polynomial P(x) with integer coefficients and a nonzero constant term, the possible rational roots are given in the form:
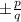
where p represents the factors of the constant term of the polynomial and q represents the factors of the leading coefficient.
SOLUTION
The polynomial is given to be:
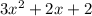
The leading coefficient is 3 and the constant term is 2.
Since all coefficients are integers, we can apply the rational zeros theorem.
The factors of the leading coefficient are 1 and 3, while the factors of the constant term are 1 and 2. Therefore, we have that:
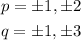
Hence, the possible roots are: