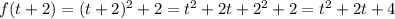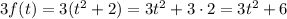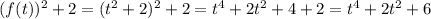Question

(1 point) If f(x) = x2 + 2, find and simplify the following:(a) f(t + 2)(b) f(t^3+ 2) =(d) 3f(t)(e) (f(t))^2 + 2 =

Answer 1

Consider the function f(x) = (x)^2+2 which is equivalent to the given function. In here, we are taking whatever is inside the the parenthesis , we raise it to the power of 2 and then add 2. Note that if we change the x for a t, we will get f(t) = (t)^2+2 which is essencially the same thing.

To solve this question we will use the following formula

`(a+b)^2=a^2+2ab+b^2`

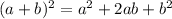
So, now we simply replace and simplify:

`f(t+2)=(t+2)^2+2=t^2+2t+2^2+2=t^2+2t+4`
`f(t^3+2)=(t^3+2)^2+2=t^6+2t^3+4+2=t^6+2t^3+6`
`3f(t)=3(t^2+2)=3t^2+3\cdot2=3t^2+6`
`(f(t))^2+2=(t^2+2)^2+2=t^4+2t^2+4+2=t^4+2t^2+6`