Question

Suppose a circular platform rotates at constant angular velocity. Does a point on the rim have radial (centripetal) and/or tangential acceleration? If the platform accelerates uniformly, does the point have radial (centripetal) and/or tangential acceleration? Explain.

Answer 1

Under constant angular velocity, there is only radial acceleration. Under changing angular velocity, there is both radial and tangential acceleration.

Step-by-step explanation:

For a circular platform rotating at constant angular velocity, a point on the rim experiences radial acceleration but not tangential acceleration.

• Radial acceleration is necessary for any object moving in a circular path to change its direction of velocity is towards the center of the circle, which is what keeps the object moving in a circle. This acceleration is given by the formula:

`a_r=(v_t^2)/(r)=r \omega ^2`

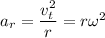
Where:

• 'a_r' is the radial (or centripetal) acceleration
• 'v_t' is the tangential (or linear) velocity
• 'r' is the radius of the curve
• 'ω' is the angular velocity

Since the angular velocity is constant, there's no change in the speed of the point along the tangent to its circular path, hence no tangential acceleration.

If the platform starts to accelerate uniformly, meaning its angular velocity is increasing, then the point on the rim has both radial and tangential acceleration. The radial acceleration continues to act towards the center of the circle to change the direction of the velocity, while the tangential acceleration acts along the tangent to the circular path, causing an increase in the linear speed of the point.

The tangential acceleration is a result of the change in angular velocity and is given by:

`a_t=r\alpha`

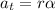
Where:

• 'a_t' is the tangential (or linear) acceleration
• 'r' is the radius of the curve
• 'α' is the angular acceleration.