Question

Dylan looked at the function
`f(x) = 4( (1)/(2) )^(x)`and said, "This function is always greater than 0, so 0 is the absolute minimum." Explain why Dylan is incorrect.

Answer 1

The function is

`f(x)=4((1)/(2))^x`

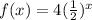
The given function is an exponential function.

A characteristic of these type of function is that it never crosses the x-axis.

If the base is between 0 and 1 and positive, then the function will be always over the x-axis.

The greater the value of x, the more close it would come to the x-axis but it will never reach it, this is called an horizontal asympote.→ since it has an horizontal asympote it will never be zero, it means that it does not have a minimum value, it just keeps decreasing until infinity.