Question

Which conic section does the equation below describe? (x-1) (+2 20 16 O A. Circle O B. Parabola O C. Ellipse O D. Hyperbola

Answer 1

It describes an hyperbola (option D)

Step-by-step explanation:

`((x-1)^2)/(20)\text{ + }((y+2)^2)/(16)\text{ = 1}`

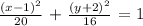
An ellipse is in the form:

`\begin{gathered} ((x-h)^2)/(a^2)\text{ + }((y-k)^2)/(b^2)\text{ = 1} \\ \text{This is not similar to the form the equation was given} \end{gathered}`

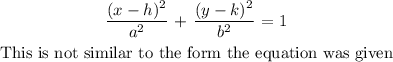
A parabola is in the form:

`\begin{gathered} a(x-h)^2=(y-k)^2 \\ \text{vertex form:} \\ y=a(x-h)^2\text{ + k} \\ \text{not similar to the equation we were given} \end{gathered}`

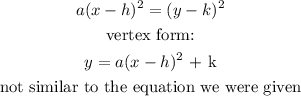
An equation of circle has a radius in the formula which is not in the given formula. Hence, it can't be circle.

An hyperbola is in the form:

`\begin{gathered} ((x-h)^2)/(a^2)\text{ - }((y-k)^2)/(b^2)\text{ = 1} \\ \text{where h = 1, k = -2, a = }\sqrt[]{20},\text{ b = }\sqrt[]{16} \\ \text{this is similar in form to the equation given} \end{gathered}`