Question

At the park there a pool shaped like a circle. A - shaped path goes around the pool. Its inner diameter is 18 yd and its outer diameter is 28 yd. 28 yd We are going to give a new layer of coating to the pathIf one gallon of coating can cover 8v * d ^ 2 how many gallons of coating we need? Note that coating comes only by the , so the number of gallons must be a whole number(Use the value 3.14 for )

Answer 1

46 gallons

Step-by-step explanation:

First, we need to calculate the area of the path. This area can be calculated as the difference between the area of the outer circle and the area of the inner circle. The area of a circle is equal to

`A=\pi r^2`

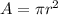
Where r is the radius. For the outer circle, the diameter is 28 yd, so the radius is equal to

radius = diameter/2

radius = 28 yd/2

radius = 14 yd

Then, the area of the outer circle is

`\begin{gathered} A=(3.14)(14\text{ yd\rparen}^2 \\ \text{ A = \lparen3.14\rparen\lparen196 yd}^2) \\ A=615.44\text{ yd}^2 \end{gathered}`

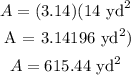
In the same way, the radius of the inner circle is

radius = diameter/2

radius = 18 yd/2

radius = 9 yd

Then, the area is

`\begin{gathered} A=(3.14)(9\text{ yd\rparen}^2 \\ A=(3.14)(81\text{ yd}^2) \\ A=254.34\text{ yd}^2 \end{gathered}`

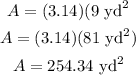
So, the area of the path is

Area path = 615.44 yd² - 254.34 yd²

Area path = 361.1 yd²

Now, we know that one gallon can cover 8 yd², so we can calculate the number of gallons as

`361.1\text{ yd}^2*\frac{1\text{ gallon}}{8\text{ yd}^2}=45.14\text{ gallons}`

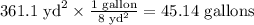
Therefore, the number of gallons is 46 because we need to round the result to a whole number.