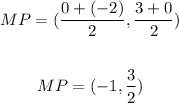Question

The graph is a straight line that passes through the points P and Q How can I state the coordinates of P and Q. How can i determine the gradient of the line segment PQ? How do I do a equation of the line PQ ? How can I find the length of Line PQ? How can I find the mid point of PQ?

Answer 1

Given the graph:

(a) The coordinates of P(x,y) and Q(x,y) are;

`P(0,3)\text{ and }Q(-2,0)`

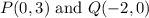
(b) The gradient, m of the line segment is;

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \\ \text{ Where }x_1=0,y_1=3,x_2=-2,y_2=0 \end{gathered}`

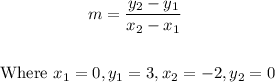
Thus;

`\begin{gathered} m=(0-3)/(-2-0) \\ \\ m=(3)/(2) \end{gathered}`

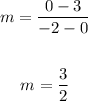
(c) The equation of the line is;

`\begin{gathered} y-y_1=m(x-x_1) \\ \\ \text{ Where }x_1=0,y_1=3,m=(3)/(2) \end{gathered}`

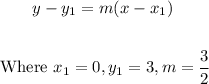
Thus;

`\begin{gathered} y-3=(3)/(2)(x-0) \\ \\ y=(3)/(2)x+3 \end{gathered}`

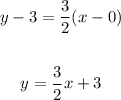
(d) The length of the line segment PQ is;

`\begin{gathered} PQ=√((x_2-x_1)^2+(y_2-y_1)^2) \\ \\ \text{ Where }x_1=0,y_1=3,x_2=-2,y_2=0 \end{gathered}`

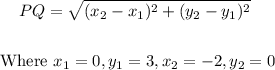
Thus;

`\begin{gathered} PQ=√((-2-0)^2+(0-3)^2) \\ \\ PQ=√(13) \end{gathered}`

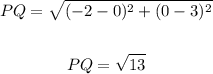
(e) The midpoint, MP of the line segment is;

`\begin{gathered} MP=((x_1+x_2)/(2),(y_1+y_2)/(2)) \\ \\ \text{ Where }x_1=0,y_1=3,x_2=-2,y_2=0 \end{gathered}`

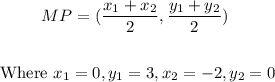
Thus;

`\begin{gathered} MP=((0+(-2))/(2),(3+0)/(2)) \\ \\ MP=(-1,(3)/(2)) \end{gathered}`