Question

In the peak season of winter days, a retailer marked the price of an electric heater as Rs 4000 and 10% discount was given to make 20% profit. But in the summer days she increased the discount percent to get only 12% profit from the same type of heater. How much did she/he increase the discount percent?

Answer 1

6%

Explanation:

The marked price of the electric heater = Rs 4000

• In winter, when 10% discount was given, the retailer made 20% profit.

• In summer, ,when the discount was increased by x%,, the retailer made 12% profit.

We want to find the value of x.

First, we find the sale price of the good after a 10% discount.

`\begin{gathered} Sale\;Price=4000-(10\%\text{ of }4000) \\ =4000-400 \\ =\$3600 \end{gathered}`

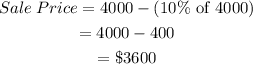
Next, the retailer made a 20% profit when he sold the heater at $3600, we find the cost price of the heater.

`\begin{gathered} \text{Percentage Profit}=\frac{\text{ Selling Price}-\text{ Cost Price}}{\text{ Cost Price}} \\ (20)/(100)=(3600-CP)/(CP) \\ 0.2=(3600-CP)/(CP) \\ \text{ Cross multiply} \\ 0.2CP=3600-CP \\ CP+0.2CP=3600 \\ 1.2CP=3600 \\ CP=(3600)/(1.2) \\ CP=3000 \end{gathered}`

The cost price of the water heater is Rs 3000.

In the summer, she increased the discount percent to get only 12% profit from the same type of heater.

We find the selling price that gives a 12% profit.

`\begin{gathered} \text{Percentage Prof}\imaginaryI\text{t}=\frac{\text{Sell}\imaginaryI\text{ng Pr}\imaginaryI\text{ce}-\text{Cost Pr}\imaginaryI\text{ce}}{\text{Cost Pr}\imaginaryI\text{ce}} \\ (12)/(100)=(SP-3000)/(3000) \\ (12)/(100)*3000=(SP-3000)/(3000)*3000 \\ 360=SP-3000 \\ SP=3000+360 \\ SP=3,360 \end{gathered}`

The selling price in summer was $3,360.

Finally, we find the discount.

`\begin{gathered} (3360)/(4000)=0.84 \\ \implies(1-0.84)*4000=3360 \\ 0.16*4000=3360 \end{gathered}`

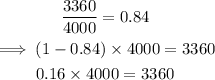
The new discount was 16%.

Therefore:

`x=16-10=6\%`

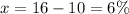
The retailer increased the discount by 6%.