SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given sides
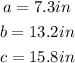
STEP 2: Write the formula to calculate the missing angles
To get the missing angles, we use the cosine laws and sine laws stated below:
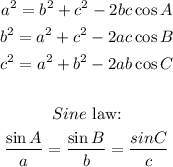
STEP 3: Use the cosine law to find the angle A

Angle A = 27.3 degrees
STEP 4: Find Angle B
Using sine rule, we have:

STEP 5: Calculate the Angle C
Recall that the sum of angles in a triangle is 180 degrees, therefore,
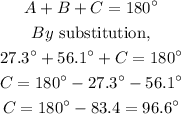
Hence, the angles are:
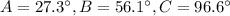
OPTION A