Final Answer:
The possible points of discontinuity for the function
 . The function is discontinuous at
. The function is discontinuous at
 with a removable discontinuity, and it is continuous at
with a removable discontinuity, and it is continuous at
 .
.
Step-by-step explanation:
The function
 is defined as follows:
is defined as follows:
\[ g(x) = \begin{cases}
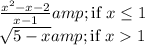
![\end{cases} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vz9gzo1z96gdahkz99pqli70ogys3tiojt.png)
Now, let's analyze the possible points of discontinuity:
1. Discontinuity at
 , the denominator becomes zero, leading to an undefined value. To determine the type of discontinuity, factorize the numerator:
, the denominator becomes zero, leading to an undefined value. To determine the type of discontinuity, factorize the numerator:
 . Canceling the common factor of
. Canceling the common factor of
 in both the numerator and denominator, we get
in both the numerator and denominator, we get
 . So, the discontinuity
. So, the discontinuity
 is removable, and
is removable, and
 can be redefined as
can be redefined as
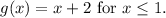
2. Discontinuity at
 , the square root term
, the square root term
 is defined for
is defined for
 , so there is no discontinuity at
, so there is no discontinuity at
 .
.
In summary, the function has a removable discontinuity at
 and is continuous at
and is continuous at
 . The redefined function is
. The redefined function is
 .
.