Question

The following data set represents the math test scores for a class of 20 students.90, 60, 85, 100, 100, 90, 100, 75, 100, 95, 95, 85, 30, 100, 40, 15, 100, 90, 70, 80Identify the best measure of central tendency for this data set.Select the correct answer below:the mode, 100the mean, 80the median, 95the median, 90the mean, 85

Answer 1

The first step to identifying the central tendency of the data set is to order the scores from least to greatest, so:

15,30,40,60,70,75,80,85,85,90,90,90,95,95,100,100,100,100,100,100

Now, the mode of a data set is the value that occurs most frequently. As we can observe in this case, the mode is 100 but is at the right extreme of the set, it is not the central tendency of the data.

The formula gives the mean:

`\bar{x}=(\sum_(i=1)^nx_i)/(n)`

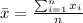
So, we need to sum all the values and divide it by the total number of values, 20:

As we can observe, the mean is a little bit far of the central tendency, given that the most frequent values are over 80.

Finally, let's check the median, and it is the value that is located at the center of the data set. As we have 20 values, the median will be the average value between the 10th and 11th terms, so:

10th term: 90

11th term:90

Median: 90.

It is more representative to the central tendency of the data se