Answer:
The acceleration of the box is approximately 3.03 m/s^2.
Step-by-step explanation:
To find the acceleration of the box, we need to resolve the gravitational force acting on the box along the ramp. The component of the gravitational force parallel to the ramp will be responsible for the acceleration.
The gravitational force acting on the box can be calculated using the formula:
force = mass × acceleration due to gravity
Given that the mass of the box is 10 kg and the acceleration due to gravity is approximately 9.8 m/s^2, we can calculate the force as follows:
force = 10 kg × 9.8 m/s^2
= 98 N
Next, we need to find the component of the force along the ramp. This can be calculated using the formula:
force along ramp = force × sin(angle of the ramp)
The angle of the ramp is given as 18 degrees. Converting this to radians gives us:
angle in radians = 18 degrees × (π/180)
= 0.314 radians
Now we can calculate the force along the ramp:
force along ramp = 98 N × sin(0.314 radians)
= 98 N × 0.309
= 30.282 N
The force along the ramp is equal to the mass of the box multiplied by the acceleration:
force along ramp = mass × acceleration
Rearranging the equation, we can solve for the acceleration:
acceleration = force along ramp / mass
= 30.282 N / 10 kg
= 3.0282 m/s^2
Therefore, the acceleration of the box is approximately 3.03 m/s^2.
To find the time it takes the box to slide 2 meters down the ramp, we can use the equation of motion:
distance = initial velocity × time + (1/2) × acceleration × time^2
Since the box starts from rest, the initial velocity is 0 m/s. Plugging in the values, we have:
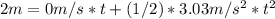
Simplifying the equation:
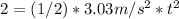
Multiplying both sides by 2 and rearranging the equation, we get:

Therefore, it takes approximately 0.8128 seconds for the box to slide 2 meters down the ramp.