To begin with, the vertices of the triangle ABC are as follows;
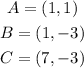
We shall label the center of the triangle (that is the circum-radius) as point O.
That means
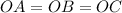
Note also that the distance between two points on a coordinate grid is given as follows;
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/uzxp21vzgmb574ylk52g.png)
That means the distance from point OA equals OB and also equals OC.
Therefore;
![\begin{gathered} OA=\sqrt[]{(x-1)^2+(y-1)^2} \\ OA^2=(\sqrt[]{(x-1)^2+(y-1)^2})^2 \\ OA^2=(x-1)^2+(y-1)^2 \\ OA^2=x^2-2x+1+y^2-2y+1 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/b7wy4mrc7n3nbk3lizru.png)
Similarly, distance OB can be calculated as follows;
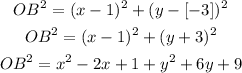
Note that
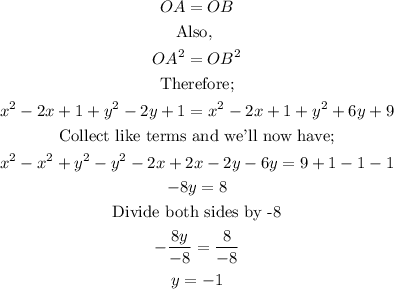
We shall now calculate the distance between point OC, as follows;
![\begin{gathered} OC=\sqrt[]{(x-7)^2+(y-\lbrack-3\rbrack)^2} \\ OC^2=(x-7)^2+(y+3)^2 \\ OC^2=x^2-14x+49+y^2+6y+9 \\ \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/hx1vr8t0ty76omvvlsi2.png)
Since;

We would now have;
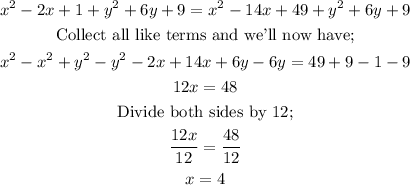
Therefore, the circumcenter of this triangle with center labelled as point O would be found at the coordinates (4, -1)
ANSWER:
