Part A:The first equation is:
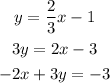
Which is the same as the second equation.
Hence the system has infinitely mant solutions.
Part B:The equations are:
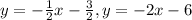
Solve the equations to get:
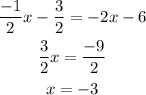
Substitute the value of x in any of the equations to get:

Hence the system has unique solution whicch is (-3,0)
Part C:The equations are:
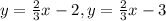
The system represents a pair of parallel lines hence the system has no solution: