Question

Its three parts to this question .The picture It's a little blurry but the graphs.System ALine 1:y=2/3x-1Line 2:-2x+3y=-3System BLine 1:-1/2x-3/2Line 2:-2x-6System CLine 1:y=2/3x-2Line 2:y=2/3x+3

Answer 1

Part A:The first equation is:

`\begin{gathered} y=(2)/(3)x-1 \\ 3y=2x-3 \\ -2x+3y=-3 \end{gathered}`

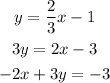
Which is the same as the second equation.

Hence the system has infinitely mant solutions.

Part B:The equations are:

`y=-(1)/(2)x-(3)/(2),y=-2x-6`

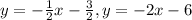
Solve the equations to get:

`\begin{gathered} (-1)/(2)x-(3)/(2)=-2x-6 \\ (3)/(2)x=(-9)/(2) \\ x=-3 \end{gathered}`

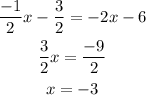
Substitute the value of x in any of the equations to get:

`y=(-1)/(2)*-3-(3)/(2)=0`

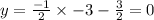
Hence the system has unique solution whicch is (-3,0)

Part C:The equations are:

`y=(2)/(3)x-2,y=(2)/(3)x-3`

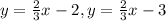
The system represents a pair of parallel lines hence the system has no solution: