Final answer:
The area of the largest square inscribed in a triangle with legs 20cm and 30cm is
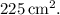
Explanation:
To find the area of the largest square inscribed in a triangle with legs 20cm and 30cm, first, we recognize that the largest square will be achieved when its diagonal coincides with the base of the triangle.
The base of the triangle is 30cm, which will be the diagonal of the inscribed square. Using the diagonal of the square and the properties of a square, we employ the formula for the area of a square
 to determine the area.
to determine the area.
Thus, with the diagonal of the square being 30cm, the area calculation yields
 which represents the maximum area achievable for the square within the given triangle.
which represents the maximum area achievable for the square within the given triangle.